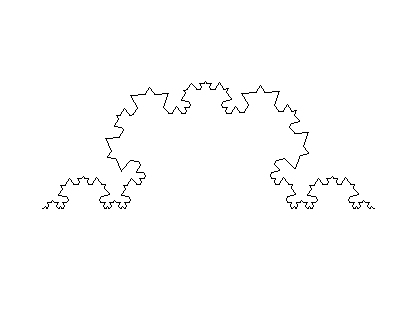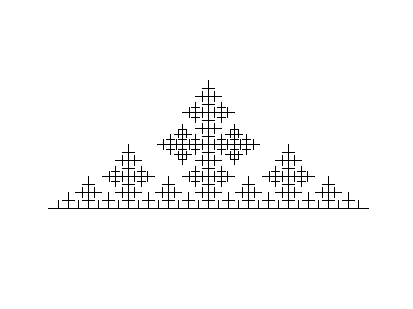Overview
The discovery of the fractal geometry of nature has caused mathematicians and scientists
to think differently about how things in the universe are structured. Fractal geometry
is now an important aspect of many scientific descriptions of natural phenomena, as well
as an important research area in mathematics. It is not easy to put a simple
answer to the question "What is a fractal?", partly because of the rich variety
of objects and phenomena that are fractal.
However, if there is a single unifying concept
to all things fractal, it is the notion of self similarity and scaling. This lesson
is intended to help students discover the concept of self similarity.
Preparation and Materials
- Images and/or objects that exhibit self similarity.
- Familiarity with use of the application Snowflake.
- A Power Macintosh with the application Snowflake loaded on
it. Alternatively, you could use any machine with a web connection and
a modern browser and connect to Snowflake
Online".
Objectives
Students will
- look at examples of naturally occuring and man made self similarity
- use a computational tool to further explore and create their own self similar objects
- practice clearly describing mathematical concepts in their own words
- make connections between mathematics and the real world
Standards
This lesson fulfills portions of the following standards and curriculum
guidelines:
- NCTM content standard
on Patterns and Functions, including:
- describe, extend, analyze, and create a wide variety of
patterns
- analyze functional relationships to explain how a change in one
quantity results in a change in another
- NCTM content standard
on Geometry, including:
- identify, describe, compare, and classify geometric figures
- visualize and represent geometric figures with special attention
to developing spatial sense
- explore transformations of geometric figures
- develop an appreciation of geometry as a means of describing
the physical world
Activities
Discussion of Similarity
Even if the students have heard of (the mathematical sense of) similarity
before, they are likely not to remember it too well. What we need for this
discussion is not the full technical definition with proportions, etc, but
the concept that object A is similar to object B if one is a "zoomed in"
version of the other. A reduction or enlargement with a copy machine
is a good example that the students may already be familiar with. In
any event, it is important that they understand what we mean by similarity
in order for self similarity to have meaning, but it is also important not
to get bogged down in defining similiarity precisely at this point.
Examination of Self Similar Items
Without bringing up the term "self similar" yet, show the students pictures of
(or, ideally, actual physical examples of) objects that exhibit self similarity.
Tell them that they should try to find some characteristic that is shared by
all of the objects. Give them time to discuss this as a class or in groups
and collect answers on the board.
Hints and Prompts
Possible prompts that could be introduced to the discussion include
- telling them the answer
- tell them that the characteristic you're looking for is called self
similarity, and ask them to try to figure out what that might mean
- visual prompt
- mark one of the pictures with a box or circle around a small copy of the
image and tell them to think about the indicated part of the picture
- further prodding
- if that's not enough, you could tell them to mentally enlarge that section
of the picture (or sketch an enlarged version) and see what they notice about
it
- grabbing the students and shaking them
- okay, not that, but do try to get them to see the idea for themselves
before giving them the answer
Discussion of Self Similarity
Tell the students that the concept of self similarity and self simillar
objects have recently caught the attention of biologists, chemists,
meteorologists, artists, musicians, and t-shirt manufacturers.
The reasons for this include
- Many objects in nature exhibit self similarity
- Some things in our bodies, like our kidneys, lungs, and circulatory systems
have a form of self similarity
- Graphic designers and artists have found ways to generate fascinating
self similar images that hadn't been thought of before
- Self similar objects have lots of neat mathematical properties
Creation of Self Similar Objects
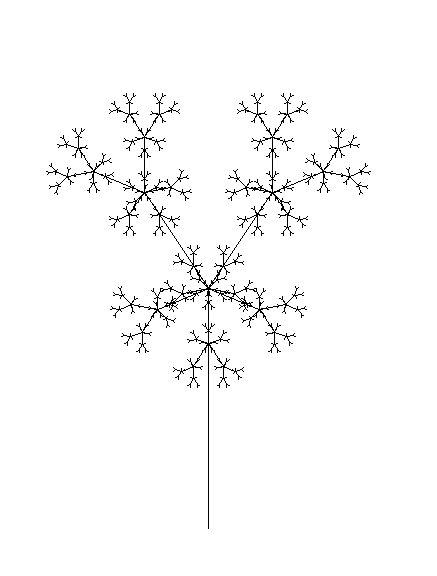
The black and white images below were created with Snowflake. Students
can use Snowflake to explore self-similarity interactively. Explain
the basic use of the program without going into detail about the actual
algorithm that generates the curves. Have them move the points around and
observe what happens, and look for examples of self similarity. Have them
save their favorite patterns, and allow each student to print out one
favorite.
Writing Assignment
Ask the students to pretend that they have to explain self similarity to
someone else their own age. In a short paper, have them describe the
concept verbally as well as using illustrations (such as their printout
or a sketch). When they have completed this assignment, have them
read their own paper,
pretending that they had never heard of self similarity before. What
should they change to make it clearer?
Go to Snowflake Curriculum Resources
 Shodor Home Page
Shodor Home Page
Last Update: May 22, 2006
© 1996, 2006 The Shodor Education Foundation, Inc.
Resources
Below are some computer-generated fractal images.
 Shodor Home Page
Shodor Home Page